Finding the "right levels" for quantization with anim GIFs
Posted: 2011-12-31T17:31:09-07:00
Okay, I'm not really getting anywhere on this thread, so I figured I would post here. I'm trying to dive deeper into the movie to anim GIF guide and trying to find ways of improving the technique using a tri-level ordered-dither. The problem is two-fold:
1. How many "levels" of colors are needed for the animation as a whole?
2. How can we leverage the average human's visual perception to add or subtract levels of different colors?
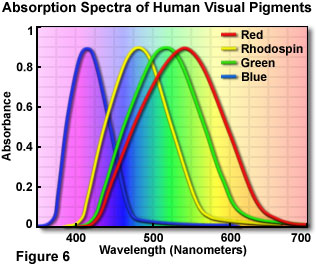
While I've dived into item #1 with only partial success, I think I'm on to something comparable with item #2. According to this article (and others), especially the graph below, humans have a harder time seeing blue than red and green, and green seems to be the easiest color to spot. (I am going to assume this applies to differences in color levels for RGB as well.) Due to the "blue" cone's absorbance towards violet (blue+red), rather than true blue, this gives red an advantage, but not as much as green.
Unfortunately, I do not have a more scientific set of mathematical ratios, but for the time being, I can use a 2:1 ratio for G:R, and a 2:1 ratio for R:B. Going back to the plane.avi, we can compare a single-level vs tri-level ordered dither:
So, we have two anim GIFs with around the same number of colors, but one is a single-level OD and the other is a tri-level OD, using the above ratio. (Because of the number of colors, the single-level had to go from 12 to 15 to match up with the number of colors, but both 12 and 15 have similar results.) What do we get? Well, the effect is subtle, but the tri-level OD appears to be of a slightly better quality than the single-level one. OD1 gives us a little bit more dither pixels that are visible to the eye. So, how can we abuse this for the full-scale 256-color GIF?
So, using all of the palette, we get a 23/23/23 at 235 colors, a 23/35/15 (1.5:1 ratio) at 252 colors, and a 21/42/10 (2:1 ratio with slight reduction of base) at 247 colors. Right off the bat, we're already squeezing more colors into the palette, due to the finer control. The images look almost identical, and the file sizes are about the same (plus or minus a few KB). Let's try lowering the tri-color base a little bit:
Awesome! We squeezed out a bunch of colors while maintaining a visually identical quality. The blue tends to get a little darker, but there isn't any signs of dithering differences. And the file sizes 646K vs. 567K/583K for 1.5/2.0:1 ratios, respectively. That's a 79K difference on the high end, with a direct translation when we OptimizeTransparency. How low can we go?
Okay, now we're starting to see some extra dithering artifacts, but the difference is very slight. However, that slight difference gives us a 506K image, which is 140K difference from the original! What about dropping the base on a single-level OD?
Is there a difference? Yes, definitely! The base 15 single OD version looks fairly crappy compared all of them. Even the base 18 single OD version, at 569K, isn't as good as the base 15 tri-color OD versions.
So, in summary, this is a valid technique to reduce the size of the animation without reducing the quality, or if you prefer, raising the quality of the image without raising the size of the animation. However, if anybody has any other clues to item #1 and the "official" ratios, I'd like to improve upon this.
1. How many "levels" of colors are needed for the animation as a whole?
2. How can we leverage the average human's visual perception to add or subtract levels of different colors?
While I've dived into item #1 with only partial success, I think I'm on to something comparable with item #2. According to this article (and others), especially the graph below, humans have a harder time seeing blue than red and green, and green seems to be the easiest color to spot. (I am going to assume this applies to differences in color levels for RGB as well.) Due to the "blue" cone's absorbance towards violet (blue+red), rather than true blue, this gives red an advantage, but not as much as green.

Unfortunately, I do not have a more scientific set of mathematical ratios, but for the time being, I can use a 2:1 ratio for G:R, and a 2:1 ratio for R:B. Going back to the plane.avi, we can compare a single-level vs tri-level ordered dither:
Code: Select all
$ convert plane.avi -ordered-dither o8x8,12,24,6 -append -format %k info:
102
$ convert plane.avi -ordered-dither o8x8,12 -append -format %k info:
73
$ convert plane.avi -ordered-dither o8x8,14 -append -format %k info:
92
$ convert plane.avi -ordered-dither o8x8,15 -append -format %k info:
109
$ convert -quiet -delay 1 plane.avi -ordered-dither o8x8,15 +map plane_od1.gif
$ convert -quiet -delay 1 plane.avi -ordered-dither o8x8,12,24,6 +map plane_od2.gif
$ cat > test.html
<img src="plane_od1.gif">
<img src="plane_od2.gif">
^D
$Code: Select all
$ convert plane.avi -ordered-dither o8x8,23 -append -format %k info:
235
$ convert plane.avi -ordered-dither o8x8,23,46,11 -append -format %k info:
288
$ convert plane.avi -ordered-dither o8x8,23,35,15 -append -format %k info:
252
$ convert plane.avi -ordered-dither o8x8,21,42,10 -append -format %k info:
247
$ convert -quiet -delay 1 plane.avi -ordered-dither o8x8,23 +map plane_od1.gif
$ convert -quiet -delay 1 plane.avi -ordered-dither o8x8,23,35,15 +map plane_od_tri1.5.gif
$ convert -quiet -delay 1 plane.avi -ordered-dither o8x8,21,42,10 +map plane_od_tri2.0.gif
$ cat > test.html
<img src="plane_od1.gif">
<img src="plane_od_tri1.5.gif">
<img src="plane_od_tri2.0.gif">
^D
$Code: Select all
$ convert plane.avi -ordered-dither o8x8,18,27,12 -append -format %k info:
160
$ convert plane.avi -ordered-dither o8x8,18,36,9 -append -format %k info:
188
$ convert -quiet -delay 1 plane.avi -ordered-dither o8x8,18,27,12 +map plane_od_tri1.5.gif
$ convert -quiet -delay 1 plane.avi -ordered-dither o8x8,18,36,9 +map plane_od_tri2.0.gifCode: Select all
$ convert plane.avi -ordered-dither o8x8,15,23,10 -append -format %k info:
128
$ convert plane.avi -ordered-dither o8x8,15,30,8 -append -format %k info:
145
$ convert -quiet -delay 1 plane.avi -ordered-dither o8x8,15,23,10 +map plane_od_tri1.5.gif
$ convert -quiet -delay 1 plane.avi -ordered-dither o8x8,15,30,8 +map plane_od_tri2.0.gifCode: Select all
$ convert plane.avi -ordered-dither o8x8,15 -append -format %k info:
109
$ convert plane.avi -ordered-dither o8x8,18 -append -format %k info:
149
$ convert -quiet -delay 1 plane.avi -ordered-dither o8x8,18 +map plane_od2.gif
$ convert -quiet -delay 1 plane.avi -ordered-dither o8x8,15 +map plane_od3.gif
$ cat > test.html
23: <img src="plane_od1.gif"><br>
18: <img src="plane_od2.gif"><br>
15: <img src="plane_od3.gif">
<img src="plane_od_tri1.5.gif">
<img src="plane_od_tri2.0.gif">So, in summary, this is a valid technique to reduce the size of the animation without reducing the quality, or if you prefer, raising the quality of the image without raising the size of the animation. However, if anybody has any other clues to item #1 and the "official" ratios, I'd like to improve upon this.